Un vistazo a las ciencias: División de Polinomios (2° Secundaria)

División de polinomios:

a. Caso general: (1)

Para dividir mediante este método se debe seguir los siguientes pasos :
Se ordena los polinomios, generalmente en forma decreciente.
Se escribe en línea horizontal uno a continuación de otro utilizando el signo de división aritmética.
Se divide el primer término del dividendo, entre el primer termino del divisor, obteniéndose el primer término del cociente.
Este término se multiplica por cada uno de los términos del divisor y se pasan a restar con los correspondientes términos del dividendo.
Se divide el primer término del resto obtenido entre el primer término del divisor y se obtienen el segundo término del cociente.
Se procede como en el pasa 4 y así sucesivamente hasta terminar la división.

Ejemplo : Hallar el cociente en la siguiente división :

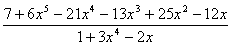
Solución: Ordenamos ambos polinomios en forma decreciente, la operación se dispone en la forma siguiente :

6x⁵– 21x⁴ – 13x³ + 25x² – 12x + 7		3x⁴ + 0x³ + 0x² – 2x + 1
- 6x⁵ – 0x⁴ – 0x³ + 4x² – 2x		2x - 7
	-21x⁴ – 13x³ + 29x² – 14x + 7
	21x⁴ + 0x³ + 0x² – 14x+ 7
	-13x³ + 29x² – 28x + 14

Donde : cociente ( q ) = 2x – 7

Residuo ( r ) = -13x³ + 29x² – 28x + 14

(1).- Metodo Clasico o Normal. División de los Polinomios. Productos notables.http://www.monografias.com/trabajos16/productos-notables/productos-notables.shtml#ESTUDIO

Referencias:

b. Aplicando el método de los coeficientes separados.

Metodod de coeficientes separados: (2)

En este caso, además de los consideraciones anteriores se debe tener en cuenta :
Se trabajan solamente con los coeficientes y sus correspondientes signos del dividendo y divisor.
En el caso de faltar un término con una potencia de la variable se coloca en su lugar cero, en el divisor.
De esta manera se obtiene los coeficientes con sus signos del polinomio cociente.

Para determinar el grado del cociente y resto se aplican las propiedades :

q° = D° - d

r° = d – 1

Este método es recomendable para polinomios de una sola variable.

Ejemplo : Efectuar la siguiente división :

Solución : Observamos que el polinomio dividendo y divisor están ordenados.

Luego :

El cociente ( q ) es de grado : q° = D° - d° = 5 – 2 = 3

El cociente es q = 2x³ – 6x² – 7x + 8

el de grado : r° = d° - 1 = 2 – 1 = 1

El resto ( r ) es de grado r = 3x – 1

(2). Metodos de loc Coeficientes Separados. Estudio de los metodos. Productos Notables. http://www.monografias.com/trabajos16/productos-notables/productos-notables.shtml#ESTUDIO

Referencias:

c. Aplicando el método de Horner

(3)

(3).- Metodo de Horner. Preprocesamiento. Algoritmos Numéricos. http://decsai.ugr.es/~verdegay/tema-15.pdf

Referencias:

d. Método de Ruffini: casos

Primero: (4)

¿Quien fue Ruffini?

El gran matemático italiano, Pablo Ruffini (1765 – 1822) ideó un procedimiento esquemático para hallar el cociente y el resto de la división de un polinomio cualquiera por otro de la forma x – a.

Este procedimiento que tiene una disposición práctica muy simple, se conoce con el nombre de

Regla de Ruffini.

Regla de Ruffini: